| �a(ch��n)Ʒ���Q: | |
| �a(ch��n)Ʒ���: | |
| �a(ch��n)ƷС�: | |
- ȫ���y(t��ng)һ�N�۟ᾀ��
- ����������
- 010-64437473
- �Ϻ���
- 021-62113795
- ���ڣ�
- 0755-86241216
�߉�ˮ��������ጷ�Ч��(y��ng)����Փ�����͉���Ӌ��
�r�g��2012-11-29 ��Դ�� http://www.icesmile.cn
ж�d�ͼ��dһ�ӿ���ʹ���d���ϰl(f��)���Ɖ���ͬ�ӣ��w����Һ�w���oˮ���������������ڏ���׃�ζ��w�e�sС�������w���Ѓ��揗�ԑ�(y��ng)׃�ܡ���(d��ng)����ͻȻጷŕr���������w���еđ�(y��ng)׃�ܕ��S֮ጷš����ڲ��ϵĿ��������h(yu��n)�h(yu��n)�����俹�����������ґ�(y��ng)׃�ܵ�ͻȻጷź͑T�����þ͕���(d��o)���w��ж�d�r������(y��ng)���Ɖġ�
�ڸ߉�ˮ�����������������w�������뵽ˮ�������������w���ܵ��oˮ�������Ӊ����߉���B(t��i)��ʹ���w����(n��i)�����кܸߵď��ԑ�(y��ng)׃����Ȼ��(j��ng)ˮ�������ٶ���ͻȻጷţ����F(xi��n)����ጷ�Ч��(y��ng)����������
����ͻȻж�d���d��ጷ�Ч��(y��ng)���҂�����ͨ�^���εď��ɼ�ж�d�^�́��f����
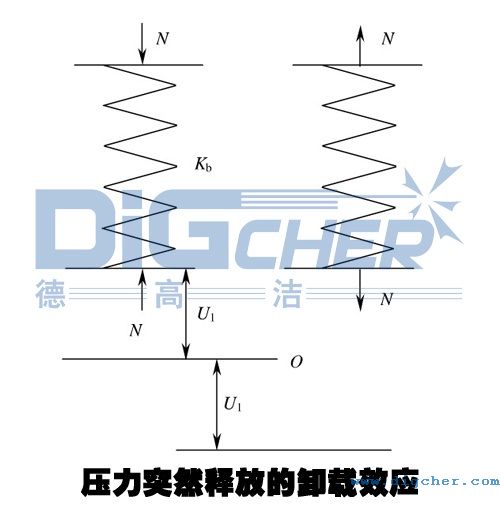
�ψD��ʾ�ď��ɣ��䄂�Ȟ� 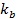 ����(d��ng)���������ϵ������� N �r�����ɶ˲������s��
����(d��ng)���������ϵ������� N �r�����ɶ˲������s�� 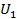 ��������(y��ng)���ɵĉ��s��(y��ng)׃�ܞ�
��������(y��ng)���ɵĉ��s��(y��ng)׃�ܞ� 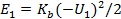 ���˕r����������� N ͻȻ��ȥ�����������������l(f��)����������������غ㣬���¶�˲�g���λ�ƿ��_(d��)ƽ��λ�� O �c���µ�
���˕r����������� N ͻȻ��ȥ�����������������l(f��)����������������غ㣬���¶�˲�g���λ�ƿ��_(d��)ƽ��λ�� O �c���µ� 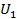 ̎��Ҳ�����fͻȻж�d���d��Ч��(y��ng)���ஔ(d��ng)�ڌ���ֵ��ͬ�ĺ��d������ӵ�������
̎��Ҳ�����fͻȻж�d���d��Ч��(y��ng)���ஔ(d��ng)�ڌ���ֵ��ͬ�ĺ��d������ӵ�������
�cԭ���d��ͬ���ǣ����d�r���ɳ��ܵ��lj���(y��ng)������ж�d�r���ɳ��ܵ�������(y��ng)�������ڿ������ȵ����俹�����ȵIJ��������É���ጷ��M(j��n)�з�������ȫ���е������H���������(sh��)���Բ��϶����п��������h(yu��n)�h(yu��n)�����俹�����ȵ�������
����(j��)�������W(xu��)��֪�����w�w�����������������䏗�ԑ�(y��ng)׃�ܲ����������_(d��)��һ���̶Ⱥ����w����(n��i)�γ��Ѽy��ʹ�Ѽy�����U(ku��)չ���M(j��n)��ʧ��(w��n)���ѡ����Ѽy�a(ch��n)���͔U(ku��)չ������ȫ���������w����(n��i)����ď��ԑ�(y��ng)׃����
���O(sh��)������������w�������ͬ�Ծ�������İ돽�� b������������ܾ����� p ������������?q��)��Q���}��ƽ���ַ��̣�
���Խ���w���ܵ��đ�(y��ng)�����_(d��)ʽ�飺
�ډ��������µđ�(y��ng)׃?y��u)�?/div>
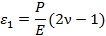 ��ʽ(3)
��ʽ(3)
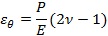 ��ʽ(4)
��ʽ(4)
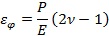 ��ʽ(5)
��ʽ(5)
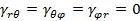 ��ʽ(6)
��ʽ(6)
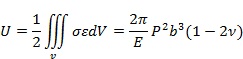 ��ʽ(7)
��ʽ(7)
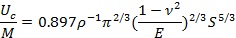 ��ʽ(8)
��ʽ(8)
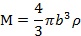 ��ʽ(9)
��ʽ(9)
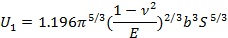 ��ʽ(10)
��ʽ(10)
�t�w���ډ��� p �����µđ�(y��ng)׃�ܞ飺
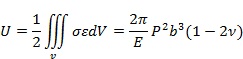 ��ʽ(7)
��ʽ(7)����(j��)�������W(xu��)�о�����(x��)ĥ�V�r���������ܶ��x�飺ݔ�뵽�����w�����_(d��)��˲�r����ď��ԑ�(y��ng)׃�������ƌ�(d��o)�ó���λ�|(zh��)���������c���ȵ��P(gu��n)ϵ�飺
���ڰ돽�� b �������w����
���빫ʽ(8)�ɵã�
��(d��ng)�w���ܵ������� p �������w��(n��i)�Ѿۼ����繫ʽ(7)��ʾ�ď��ԑ�(y��ng)׃��������������� p ͻȻጷţ��t���w��(n��i)�����F(xi��n)���쑪(y��ng)������ˣ��w�����ܵđ�(y��ng)��ֻҪ�_(d��)�����ϵ����쏊�Ⱦ͕����Ɖ������ԣ���ʽ(10)�ď��� S �Ϳ��ò��ϵ����쏊�� σl ���������t��ʽ(10)��׃?y��u)�?/div>
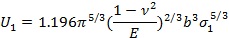 ��ʽ(11)
��ʽ(11)
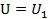 ��ʽ(12)
��ʽ(12)
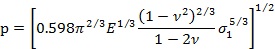 ��ʽ(12)
��ʽ(12)
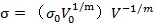 ��ʽ(13)
��ʽ(13)
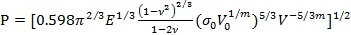 ��ʽ(14)
��ʽ(14)
�O(sh��)�e�����w����(n��i)�ď���׃��������ጷŕrȫ���D(zhu��n)׃?y��u)��w���������ܣ�
����
��ʽ(12)�f���w���ډ���ͻȻጷŕr�õ��Ɖģ���o�������w���ľ����� p �ı��_(d��)ʽ��
������]�����S�w�e��׃�Q���t�o���ď����P(gu��n)ϵ�飺
����
��ʽ����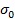 —��λ�w�eԇ��
—��λ�w�eԇ�� 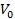 �����쏊����
�����쏊����
m —���ϵľ�����ϵ��(sh��)��
��ʽ(14)������Ҫʹ�돽�� b �������w���܉�ጷŷ�������ĉ�����ֻ�c�w�����ϵ��������W(xu��)���Ժ͎γߴ����P(gu��n)��
�ɴ˿�֪��ͨ�^����ጷŷ�����������ĉ����Ȳ��ϵĿ������ȸߣ���Ҫ�Ȳ��ϵĿ������ȵͺܶ���ͬ�r���������w���ϵľ�����Խ�����e�����w����(n��i)�ď��ԑ�(y��ng)׃�ܾ�Խ��������ጷź�ķ���Ч����Խ����
- ��(bi��o)����
- ��Փ����
- ����Ӌ��
- �߉�ˮ����
- ����ጷ�Ч��(y��ng)
��Ч��߇�������Ďׂ�����
2017-08-14
�߉���ϴ�C��ϴ�C������֮�����ϴ���ȵ�
2012-09-18
�߉�ˮ��������������y
2013-05-03
�߉���ϴ�C�M(j��n)ˮǻ�ܷ�ʧЧ��ԭ�����
2013-06-29
�߉���ϴ�C�߉��z�ܶΉ����pʧ��Փ����
2012-07-06
�߉���ϴ�C�ճ��S�o(h��)�������ĥ�p���ؼ���
2018-08-22
�߉�ˮȥë�̙C���Ç����B
2018-07-16
�߉�ˮ��������������ă�(y��u)�c
2018-07-04
�߉���ϴ�C�ڹܵ���ϴ�r��ע�����
2018-06-28
�߉�ˮ������ϴ��ȫע�����
2018-06-20



